untitled

Our department asked for an image for a post on this manuscript.

Semigraphics, ANSI, unicode, and an Arduino LCD-screen terminal

(github repo is here)

I've been playing with retro-styled interfaces terminal lately. The unicode box and block drawing characters are wonderful for this, especially "symbols for legacy computing" . These include characters from classic computers of the twentieth century, and the block-diagonal teletext characters.

These can be combined with ANSI escape codes for styled and colored text. Which all led me to ask: How hard would it be to support these features on an Arduino terminal display? This question led me down a rabbit-hole of vt100 terminal emulators on the Arduino. 

Terminal color waterfall

Some days you just need... 

 

If you have Python3 installed...

Plot the price of bitcoin directly on the command line

Here's a python script to plot the price of cryptocurrencies directly on the command line. 

This a single python script, which depends on the requests, pandas, and numpy packages. It uses the Symbols for Legacy Computing unicode block for plotting directly inside the terminal emulator. Most terminals based on the Gnome terminal support these characters.

I make no apologies for the garish color scheme, which is based on what I imagine people in the 1980s imagined the future would look like. You can edit the ANSI color codes in the source to suit.

This pulls price data from the Kraken exchange, but it is not affiliated with Kraken in any way. It's intended as a minimal demo of interfacing with Kraken's REST API, as well as a demonstration of the possibilities of semigraphics characters in modern terminal emulators.

To changes colors, styles, defaults, etc, edit the python source code. This is provided as a self-contained demonstration of calling Kraken's REST API and plotting using unicode characters in the command line. The expectation is that users will modify/incorporate parts of this into their own script.

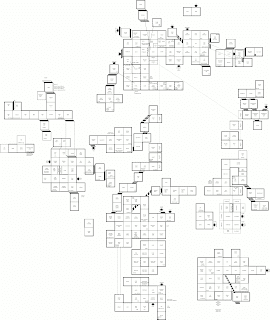
Ray's Maze, after all these years

In 1986, Silicon Beach Software released World Builder, software for creating adventure games with a text interface and accompanying black-and-white graphics.

Four years later, Ray Dunakin released "Ray's Maze", a World Builder-based puzzle game that was both addictive and immersive, despite (or perhaps because of?) the primitive graphics. Ray would go on to release two sequals in the same universe, "Another Fine Mess" (1992) and "A Mess O’ Trouble" (1994).

The games found me via mail-order shareware floppy disks circa 1998. I played them for hours, days, months on end. I never beat a single one. They can be downloaded, but are hard to play without a classic macintosh. "A Mess O’ Trouble" has been ported to run on modern macs.

Now, decades later, I have managed to beat one of these games: "Another Fine Mess" (with the exception of one puzzle). 

... On "Ray's Maze" I can't figure out how to kill the lava monster or what the balloon is for.

... On "A Mess O’ Trouble", I payed for the latest mac port, which includes an invaluable book of hints and maps. I remember playing through nearly all of it, but I can't remember how it ends or whether I ultimately finished it.

The community of players has all-but vanished, but to me these games are still better than many modern releases.

If anyone else is our there, still playing, thirty years later, I've drawn up a map of the parts of Ray's maze that I've been able to access. Perhaps we may yet learn how it ends.

 

Inverse of a 3×3 block matrix

Random noise textures on the GPU in WebGL

Procedural rendering routines often need pseudorandom numbers. For graphics rendering, we usually prefer correct-ish and fast code over properly "correct" code. My approach to random number generation is usually to intermittently seed a weak pseudo-random number generator, like a linear-feedback shift register, from a stronger source like Javascript's Math.random(). 

On the GPU, things are not so simple: we want a pseudorandom algorithm that is fast, local, and parallel. For compatibility, we should also have this RNG use an 8-bit RGBA texture for its internal state. Bitops are a bit tricky in WebGL shaders (though not impossible), so we'll use a linear congruential generator.