Optogenetic Stimulation Shifts the Excitability of Cerebral Cortex from Type I to Type II: Oscillation Onset and Wave Propagation

Our new paper, Stewart Heitmann et al. [PDF], is finally out! It's a collaboration between the theoretical neuroscientists Stewart Heitmann and Bard Ermentrout at the University of Pittsburgh, and the Truccolo lab at Brown University. 

This work could help us understand what happens when we stimulate cerebral cortex in primates using optogenetics. Modeling how the brain responds to stimulation is important for learning how to use this new technology to control neural activity.

Optogenetic stimulation elicits gamma (~50 Hz) oscillations, the amplitude of which grows with the intensity of light stimulation. However, traveling waves away from the stimulation site also emerge. It's difficult to reconcile oscillatory and traveling-wave dynamics in neural field models, but Heitmann et al. arrive at a surprising and testable prediction: 

The observed effects can be explained by paradoxical recruitment of inhibition at low levels of stimulation, which changes cortex from a wave-propagating medium to an oscillator. 

At higher stimulation levels, excitation overwhelms inhibition, giving rise to the observed gamma oscillations. Many thanks to Stewart Heitmann, Wilson Truccolo, and Bard Ermentrout. The paper can be cited as:

Heitmann, S., Rule, M., Truccolo, W. and Ermentrout, B., 2017. Optogenetic stimulation shifts the excitability of cerebral cortex from type I to type II: oscillation onset and wave propagation. PLoS computational biology, 13(1), p.e1005349.

 

 

Phase-triggered wave animation loops

The model predicts high-frequency (60-120 Hz) gamma oscillations within the stimulated area. It also predicts that these waves should propagate into the neighboring tissue, but at half this frequency. The result is that every-other wave in the stimulated area "sheds" a travelling wave into the areas nearby. 

A re-analysis of the data recorded in Lu et al. confirms that this phenomenon is also present in vivo. The GIFs below show the waves evoked by optogenetic stimulation. These loops represent an average of the phase-locked Local Field Potential (LFP) activity in a 4×4 mm patch of primate motor cortex. On the left, we see the broadband LFP, which contains contributions from both high- and low-frequency gamma oscillations. The middle and right panels show narrow-band filtered low- and high-gamma, respectively, revealing the 2:1 mode locking.

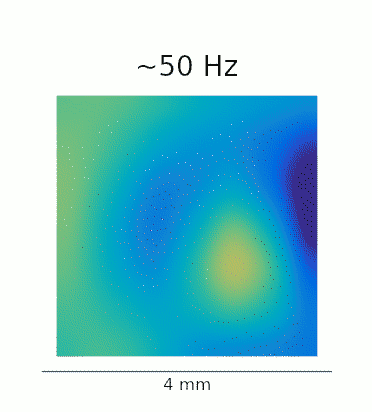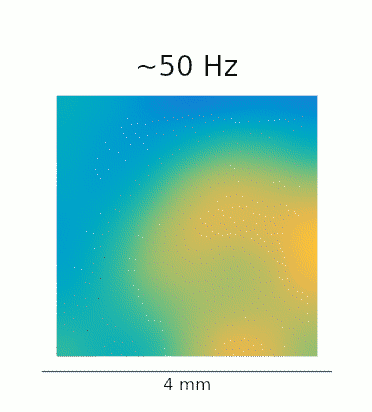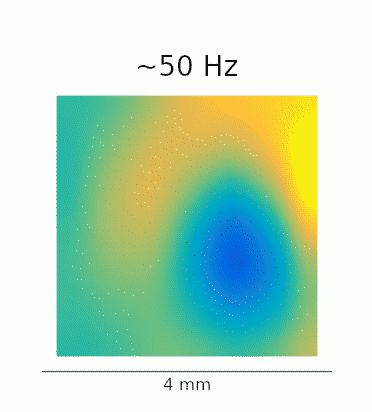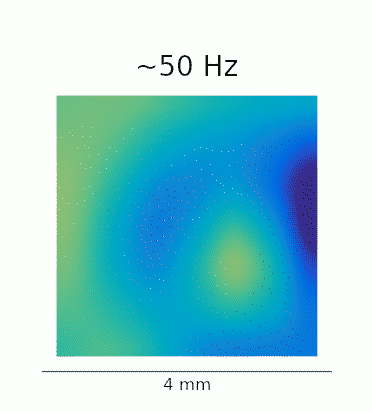
Javascript demos of the neural field model

A javascript demo of the neural field model in this paper is available on Github.  Move the slider at the base to change the intensity of the optogenetic stimulation.

 

 

 

I've also prepared a more comprehensive simulation that lets you explore how the neural field dynamics change as various parameters are altered: 

Many thanks again to Stewart Heitmann, Wilson Truccolo, and Bard Ermentrout. 

Wilson-Cowan neural fields in WebGL

Update: Dropbox no longer serves live pages from their public folders, so hosting has moved to Github. Basic WebGL example have moved to the "webgpgpu" repository, including the psychedelic example pictured to the left. Additional neural field models are hosted at the "neuralfield" repository. 

WebGL offers a simple way to write portable general-purpose GPU (GPGPU) code with visualization. The Github repository WebGPGPU walks through a series of examples to bring up a port of Wilson-Cowan neural field equations in WebGL.

The Wilson-Cowan equations are a mean-field approximation of neural activity under the assumption that spiking is asynchronous, and that observations are averaged over a large number of uncorrelated neurons. Wilson-Cowan neural fields have been used to describe visual hallucinations, flicker phosphines, and many other wave phenomena in the brain.


The Wilson-Cowan simulation demo is rudimentary at the moment, but contains a couple presets and rich and diverse dynamics are possibly by varying parameters. For entertainment, there is also an example of a full-screen pattern forming system mapped to (approximate) retinal coordinates using the log-polar transform.

Other cool WebGL implementations pattern-forming systems include the Gray-Scott reaction diffusion equations by pnmeila and Felix Woitzel's reaction diffusion and fluid dynamics simulations. Robin Houston's reaction diffusion implementation is also a good reference example for learning WebGL coding, and Robter Muth's smoothlife implementation is mesmerizing. The hope is that the examples in the WebGPGPU project provide a walk-through for how to build similar simulations in WebGL, something that is not immediately obvious if following existing WebGL tutorials.

Technical notes

I've avoided using extensions like floating point textures that aren't universally supported. Hopefully the examples in WebGPGPU will run on most systems, but compatibility issues likely remain.

Most of the examples store floating point values in 8-bit integers. This works for the firing rate version of the Wilson-Cowan equations because the firing rate is bounded between 0 and 1, so fixed precision is adequate. There are some caveats here. For example, how floating point operations are implemented, and how floats are rounded when being stored in 8-bit values, are implementation dependent. These simulations a quite sensitive to parameters and rounding errors, so different implementations can lead to different emergent dynamics. A partial workaround is to manually control how floats are quantized into 8-bit values. Floats can also be stored in 16 or 32 bit fixed-point precision, at the cost of performance. My understanding is that the default precision for fast floating point operations on the GPU is fairly low, such that 16 bits can capture all of the available precision for the [0,1] range.

The quantization of state variables can lead to numerical errors if the integration step size is too small relative to the timescales of the system. In short, if states are changing too slowly, their increments becomes smaller than 1/256, and numerical accuracy degrades because state changes are rounded-out. Moving to 16-bit precision lessens this issue, but at a cost of an approximately 2-fold slowdown, and so is not implemented except in one example.

Working with the WebGL library feels quite clumsy, because in essence the API exposes the GPU as a state machine. WebGPGPU includes some libraries that hide a lot of the boilerplate and expose a more functional interface for GPU shaders (kernels). For simulations on a grid, there is additional boilerplate to gain access to single pixes. One must tile the viewport with polygons, provide a default fragment shader, and set the viewport and canvas sizes to match the on-screen size. WebGPGPU hides this difficulty, but also walks through this process in the early examples to make it clear what is really happening.

Passing parameters to shaders involves a fair amount of overhead in Javascript, which becomes prohibitive for shaders with a large number of parameters. However, compiling shaders has relatively little Javascript overhead. In practice it is faster to include scalar parameters as #defines rather than pass them as uniforms. WebGPGPU contains some routines to phrase shader compilation as a sort of 'partial evaluation'.

This is a work in progress.